Matemáticas - Relaciones de proporcionalidad
Proporcionalidad directa: ¿Qué es? ¿Para qué sirve?
Una magnitud es aquello que se puede medir. Por ejemplo, el peso de una persona, el número de albañiles trabajando, el número de plátanos, la cantidad de pienso que come un perro, la distancia entre dos pueblos o la velocidad de un caballo al galopar.
Todas estas magnitudes se pueden relacionar con otras.
Para que dos magnitudes mantengan una relación de proporcionalidad directa tienen que estar relacionadas de tal forma que si duplicamos una, la otra se tiene que duplicar, si la triplicamos la otra también y si la reducimos a la mitad la otra también se tiene que reducir. Se puede entender que si aumentamos la cantidad de una, la otra tiene que aumentar también proporcionalmente.
¿Qué relación podemos ver entre el número de plátanos y el número de cajas que necesitamos para guardarlos?
Se puede observar que cuantos más plátanos tenemos más cajas necesitamos, ¿verdad? Estas dos magnitudes mantienen una relación proporcionalmente directa.
Es importante saber que el cociente (razón o proporción) entre dos magnitudes directamente proporcionales es siempre constante. En nuestro ejemplo tenemos que la razón es 3.
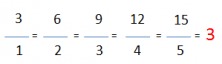
Las relaciones de proporcionalidad aparecen con mucha frecuencia en nuestra vida cotidiana.
¿Alguna vez haz comprado caramelos? ¿Cómo calculas la cantidad de dinero que tienes que pagar por los caramelos?
¿Qué puedes decir de estas dos magnitudes, el número de cerdos y el número de pacas de paja que se necesita para alimentarlos?

¿Podías decir que mantienen una proporcionalidad directa?
Tarea:
1. Si 1 kg de peras me cuesta 15 pesos. ¿Cuánto me cuestan 2 kg?
Se puede plantear una regla de 3 para resolver:
1 kg ---> 15
2 Kg --- x
x = (2)(15)/1 = 30
1 kg ---> 15
2 Kg --- x
x = (2)(15)/1 = 30
|
Kilos de peras
|
1
|
2
|
3
|
5
|
10
|
|
Precio
|
15
|
30
|
|
|
|
2. Una rueda da 200 vueltas en 10 minutos. Completa la tabla con los valores que faltan.
|
Vueltas
|
50
|
100
|
200
|
300
|
500
|
|
Tiempo
|
|
|
10
|
|
|
3. Si un dólar vale 22 pesos. ¿Cuántos dólares podré tener con 3300 pesos?
Completa la tabla
|
Dólares
|
1
|
5
|
50
|
|
|
|
Pesos
|
22
|
|
|
3300
|
5000
|
Enviar a: cecasnet3@gmail.com
Fecha: 5/junio



Comentarios
Publicar un comentario